#The resting membrane potential

The resting membrane potential is the voltage (charge) difference across a cell membrane when the cell is at rest.

It varies by cell type between -20mV and -100mV

• neuron: -70mV
• cardiac: -90mV

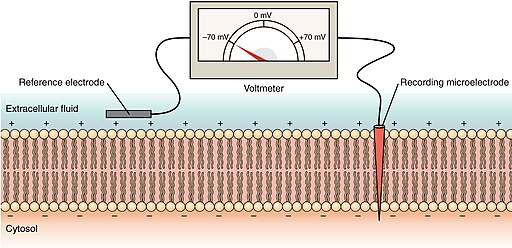
Resting membrane potential by OpenStax CC BY 4.0 via Wikimedia Commons

#Determinants of the resting membrane potential

The resting membrane potential is influenced by processes that create electrochemical gradients across a cell membrane:

• selective permeability of a cell membrane to certain ions
  • e.g. cells are relatively impermeable to Na+
  • contributes to the concentration gradient of Na+ (more in ECF), which in turn creates an electrical potential across the cell membrane
• active transport
  • energy dependent process that moves ions against their electrical or concentration gradient
  • e.g. Na/K-ATPase pump
    • moves 3Na+ out of cell and 2K+ into cell against their electrochemical gradients
    • the net efflux of cations produces an electrical gradient, contributing to the negative resting membrane potential
• the Gibbs-Donnan effect

#Nernst potentials

The Nernst potential of an ion describes the potential difference that opposes the chemical concentration gradient of the ion when there is no net movement of that ion across the cell membrane, if it is permeable to that ion.

Let's use the K+ ion as an example.

• K+ is abundant within the cell (~150mmol/L) and scant outside the cell (~4mmol/L)
• this creates an concentration gradient that wants to push K+ out of the cell
• to prevent an efflux of K+, there must be an electrical gradient opposing the concentration gradient, such that there is no net movement
• for K+, that occurs with a membrane potential of approximately -90mV
• this is known as its equilibrium potential or Nernst potential and is expressed as $E_\text{K} \approx -90\text{mV}$

Calculation of the Nernst potential assumes that the cell membrane is permeant to that ion. Nernst potentials of ions that are able to move freely (e.g. K+, Cl-) therefore approximate the actual membrane potential more closely.

Nernst potentials for important ions:

• $E_\text{K} \approx -90\text{mV}$
• $E_\text{Cl} \approx -70\text{mV}$
• $E_\text{Na} \approx +60\text{mV}$

#Nernst equation

The aptly named Nernst equation calculates the Nernst potential. Knowing this equation would be considered by some to be completely irrelevant to the practice of intensive care. However, the college is not above requesting this information from exam candidates, stating in 2024B that 'better responses were able to use the correct eponym, constants and/or logarithmic transformation (from the ln to log10).'

The Nernst equation for a given ion:

$$E = {RT\over zF} \ln\Bigg({[\text{ion}]_{\text{out}}\over[\text{ion}]_{\text{in}}}\Bigg) \approx 58 \log_{10}\Bigg({[\text{ion}]_{\text{out}}\over[\text{ion}]_{\text{in}}}\Bigg) \text{mV}$$

• $R$ = universal gas constant
• $T$ = temperature in Kelvin
• $z$ = valance of the ion (i.e. +1 for K+, -1 for Cl-)
• $F$ = Faraday's constant (relates charge to the concentration of electrons)

#The Goldman-Hodgkin-Katz equation

As alluded to earlier, the permeability of the cell membrane to a particular ion increases its contribution to the membrane potential. More permeant ions (K+, Cl-) contribute more than less permeant ions (Na+).

This makes intuitive sense. If an ion is impermeant, it is always at equilibrium as there is never any net movement across the cell membrane. Therefore no opposing electrical potential is required to balance its concentration gradient.

You might then conclude that incorporating ion permeability into the Nernst equation would yield an accurate calculation for the membrane potential.

Enter the Goldman-Hodgkin-Katz equation (aka the Goldman equation). It takes into account the effect of all ions and their permeability simultaneously to do exactly that:

$$\begin{align*} V_m &= {RT\over F} \ln\Bigg({P_\text{K}[\text{K}^+]_{\text{out}} + P_\text{Na}[\text{Na}^+]_{\text{out} } + P_\text{Cl}[\text{Cl}^-]_{\text{in}}\over P_\text{K}[\text{K}^+]_{\text{in}} + P_\text{Na}[\text{Na}^+]_{\text{in} } + P_\text{Cl}[\text{Cl}^-]_{\text{out}}}\Bigg) \\ &\approx 58 \log_{10} \Bigg({P_\text{K}[\text{K}^+]_{\text{out}} + P_\text{Na}[\text{Na}^+]_{\text{out} } + P_\text{Cl}[\text{Cl}^-]_{\text{in}}\over P_\text{K}[\text{K}^+]_{\text{in}} + P_\text{Na}[\text{Na}^+]_{\text{in} } + P_\text{Cl}[\text{Cl}^-]_{\text{out}}}\Bigg) \text{mV} \end{align*}$$

• $V_m$ = the membrane potential
• $P$ = the permeability of each ion, which may change, for example when a voltage gated Na+ channel is opened
• note that the in/out for negatively charged ions is reversed